Ok, I was nerd-sniped by the problem at https://xkcd.com/356/ . But I’m wondering if I managed to survive it somehow.

Let’s first number all the nodes systematically. We’ll number them as \(A_{(i,j)}\) where \(i\) and \(j\) give the x index and y index respectively. So now, we’re asked to find the effective resistance between \(A_{(0,0)}\) and \(A_{(2,1)}\).

The case where you’re asked to find the effective resistance between two adjacent nodes \(A_{(0,0)}\) and \(A_{(1,0)}\) is a common one that’s solved as a superposition of two current distributions, one symmetrically spreading out from \(A_{(0,0)}\) and the other symmetrically converging into \(A_{(1,0)}\). This gives us an effective resistance of \(R/2\) for that case, since the current in the arm connecting \(A_{(0,0)}\) and \(A_{(1,0)}\) is seen to be \(I/2\).

Let’s do a similar thing for the xkcd case and first consider a current \(I\) coming into \(A_{(0,0)}\) and symmetrically spreading out. As shown in the figure below –

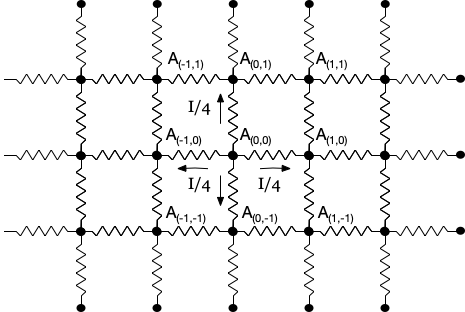
We now need to figure out the current flow through other nodes as well, in particular through \(A_{(1,0)}-A_{(1,1)}\) and \(A_{(1,1)}-A_{(1,2)}\). If we consider the box \(B\) shown below, extended all the way vertically to infinity, we can see that all currents in resistors that cut through its boundary must be flowing out of the box.

We also see that the sum of all these currents must equal \(I\). Towards figuring that out, let’s look at the flow at the nodes \(A_{(0,j)}\).

Assuming a current \(c_j\) flows into \(A_{(0,j)}\) from below (taking \(j > 0\)), if we take that a fraction \(\alpha\) of this current exits \(A_{(0,j)}\) above, then the current in the upper arm is \(\alpha c_j\) for some \(\alpha < 1\) and the current out of the left and right arms are \(\frac{1-\alpha}{2}c_j\). At this point, the \(\alpha\) can be expected to vary with \(j\), but for the moment, suppose it were a constant independent of \(j\). Is there a particular value of \(\alpha\) that would be consistent with this scenario?

The first consistency condition we have is that the sum of all currents flowing out of box \(B\) must equal \(I\). The total current is given by –

\[I = 2 \times \{\frac{I}{4} + 2 \times \frac{(1-\alpha)}{2}\frac{I}{4}(1 + \alpha + \alpha^2 + \alpha^3 + …)\}\]

In the above expression, the outer \(2 \times\) is for the left-right symmetry and the inner \(2 \times\) is for the top-bottom symmetry. This sum turns out to be independent of \(\alpha\) and indeed sums to \(I\), using the identity –

\[1 + \alpha + \alpha^2 + \alpha^3 + … = \frac{1}{1-\alpha}\]

(This shouldn’t be surprising because it is practically by construction. We’ve ensured that charge is conserved at all the internal nodes irrespective of \(\alpha\) by choosing currents to sum to \(0\) at each node, and so the exiting current must sum to \(I\). Still, good to see that that checks out even when written out explicitly.)

The current pattern at \(A_{(1,1)}\) should have reflection symmetry around the line joining \(A_{(0,0)}-A_{(1,1)}\). So the current in the arms joined at \(A_{(1,1)}\) must be as shown below –

So the incoming current pattern at \(A_{(1,2)}\) should look like this, putting our earlier assumption about the constant \(\alpha\) to work.

If we then consider the box spanned by \(A_{(0,1)}\) and \(A_{(1,2)}\), we have another consistency condition, that the potential difference between \(A_{(0,1)}\) and \(A_{(1,2)}\) must be the same whether we calculate it using the upper path or the lower path, according to the diagram below –

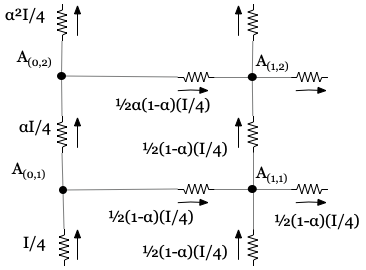
That consistency condition then gives us –

\[\frac{\alpha IR}{4} + \frac{\alpha(1-\alpha)}{2}\frac{IR}{4} = 2 \times \frac{1}{2}\frac{(1-\alpha)IR}{4}\]

Cancelling \(IR\) and multiplying by 8 throughout, we get –

\[2\alpha + \alpha(1-\alpha) = 2(1-\alpha)\]

i.e.

\[\alpha^2 - 5\alpha + 2 = 0\]

Solving that, and restricting to \(0 < \alpha < 1\), we have –

\[\alpha = \frac{5 - \sqrt{5^2 - 4\times 2}}{2} = \frac{5-\sqrt{17}}{2}\]

So now the potential difference \(V\) between \(A_{(0,0)}\) and \(A_{(2,1)}\) is given by –

\[V^+ = \frac{IR}{4} + 2 \times \frac{(1-\alpha)}{2}\frac{IR}{4}\]

Similarly, for the superimposed current pattern with \(I\) drawn at \(A_{(2,1)}\),

\[V^- = \frac{IR}{4} + 2 \times \frac{(1-\alpha)}{2}\frac{IR}{4}\]

So the total potential difference in the superimposed picture is –

\[V = V^+ + V^- = \frac{IR}{2} + (1-\alpha)\frac{IR}{2} = IR(1-\frac{\alpha}{2})\]

So the effective resistance between \(A_{(0,0)}\) and \(A_{(2,1)}\) must be given by –

\[R_{\text{eff}} = (1 - \frac{5-\sqrt{17}}{4})R = \frac{\sqrt{17}-1}{4}R \approx 0.7808 R \]

All of this hinges on \(\alpha\) being independent of \(j\), for which I don’t have a good argument, except that it seems reasonable to expect it, given that from the perspective of the node \(A_{(0,j)}\), looking away from \(A_{(0,0)}\), it always looks the same no matter how many steps we take. Maybe that’s sufficient, but I’m still not too comfortable with that yet.

Let me know whether this calculation is correct or not in the comments. Or more importantly, let me know if anyone actually managed to measure this kind of an effective resistance.

Now, the real nerd-snipe would be to find out the effective resistance between \(A_{(0,0)}\) and \(A_{(i,j)}\) in general, for \((i,j) \neq (0,0)\).

What is the core of the problem?

What we really need to find out here is the answer to this question –

If we hold the potential at \(A_{(0,0)}\) at \(V_0\) and the potential at infinity at \(0\), what is the potential at any other node \(A_{(i,j)}\) after a sufficiently long time? – i.e. at steady state.

Given this steady state potential distribution \(V(i,j)\), we can determine the effective resistance between any two points \((0,0)\) and \((i,j)\) using –

\[R_{\text{eff}} = 2R \times \frac{V_0 - V(i,j)}{4V_0 - V(1,0) - V(-1,0) - V(0,1) - V(0,-1)}\]

which simplifies to –

\[R_{\text{eff}} = \frac{R}{2} \times \frac{V_0 - V(i,j)}{V_0 - V(1,0)}\]

So how do we calculate the potential distribution \(V(i,j)\)? For that, we need to note that charge conservation at each node (except \((0,0)\) where we’re injecting current) gives us –

\[V(i+1,j) + V(i-1,j) + V(i,j+1) + V(i,j-1) = 4 V(i,j) \text{ for } (i,j) \neq (0,0)\]

That is a discrete version of the laplace equation, with \(V(0,0) = V_0\) and \(V(\infty,j) = V(i,\infty) = 0\) as the boundary conditions. We also have some symmetry considerations owing to the geometry of the arrangement –

\[V(i,j) = V(j,i) = V(|i|,|j|)\]

We could solve this numerically for finite grids, but can we obtain a closed form solution for \(V(i,j)\)?

Solving it numerically (even if inefficiently) for finite grids just involves iterating using the equation below, given \(V(0,0) = V_0\) –

\[V_{t+1}(i,j) = \frac{1}{4}(V_t(i+1,j) + V_t(i-1,j) + V_t(i,j+1) + V_t(i,j-1)) \text{ for } (i,j) \neq (0,0)\]

Addendum

There is another more complete (?) treatment available here - https://www.mathpages.com/home/kmath668/kmath668.htm . Thanks to my colleague Shravan Mohan for pointing me to this.